Authors:
(1) Deborah Miori, Mathematical Institute, University of Oxford, Oxford, UK and 2Oxford-Man Institute of Quantitative Finance, Oxford, UK (Corresponding author: Deborah Miori, deborah.miori@maths.ox.ac.uk);
(2) Constantin Petrov, Fidelity Investments, London, UK.
Table of Links
Conclusions, Acknowledgements, and References
4 Results
4.1 Word2vec benchmark

We begin by considering both the GoogleNews and FinText pretrained word embeddings, and find the vector representative of each one of our keywords (entities or concepts) identified within news. Unfortunately, only ∼ 30% of entities are found to have an associated vector in the GoogleNews model, while this percentage increases to ∼ 50% with the FinText model. This is due to a mixture of such models being trained on obsolete data, and inadequate complexity in our keywords being sometimes composed by multiple words. Importantly, “concepts” are further found to be strongly higher in complexity and structure rather than “entities”, and consequently of lower utility. Thus, our study will focus on “entities” as keywords for any following experiment.
We take advantage of the two selected vector embeddings to build a benchmark on the main topics addressed by our news articles. For each embedding model separately and each week of data, we complete the following steps:
-
We consider the vectors for the three most important entities (by the GPT ranking) in each article of the week. The full set of five entities is not taken, in order to produce more focused results due to the large percentage of missing vectors.
-
We cluster the found vectors by performing hierarchical clustering, which iteratively aggregates input coordinates according to some measure of similarity or distance. Since our vectors lie on a 300-dimensional space, we use the “average” method with cosine distance to complete this task (i.e. the distance between two clusters is computed as the average of all cosine distances between pairs of objects belonging to the two clusters).

-
For each cluster, we consider all the words belonging to it and compute the related centroid by averaging their vectors. We save only clusters with more than one point belonging to them.
-
To map back centroids to words, we compute the cosine distance between the centroid vector and each one of our word vectors belonging to the cluster. The word that is found to lie closer to the centroid is taken as the representative of the cluster, and by extension as representative of the “topic” discussed within the cluster.
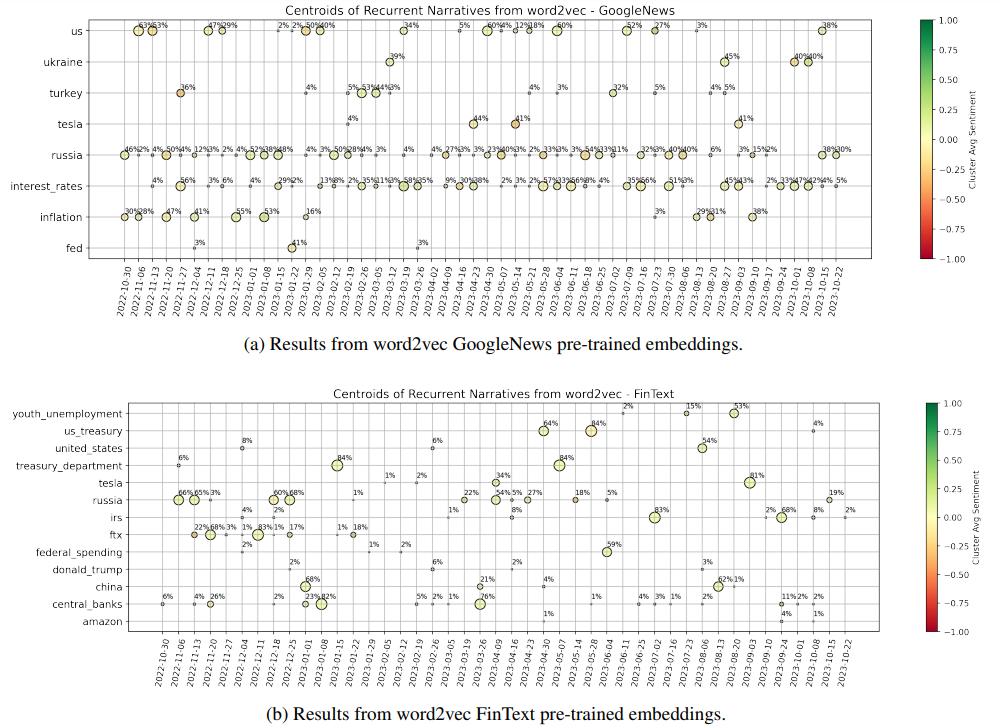
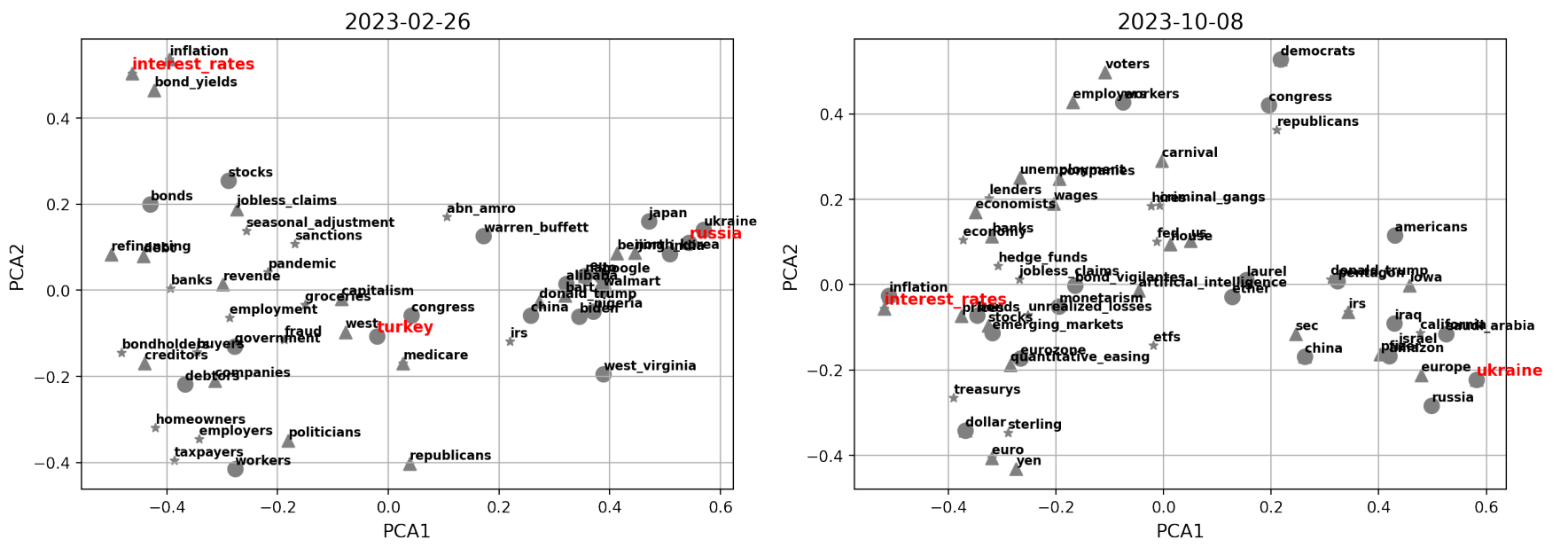
The results for both embedding models are shown in Fig. 2, for the latest one-year interval defined by weeks ending on 2022-10-30 and 2023-10-22, where we can clearly notice some signs of the different training that the models were subjected to. The GoogleNews model highlights two main narratives characteristic of the year we are considering, i.e. “Russia” (as for the war with Ukraine and associated consequences), and “interest rates” (due to continuous hiking of central banks). Interestingly, “inflation” is also a topic of main concern especially at the beginning of the data sample, and it is accurate to see that “Turkey” is signalled in February 2023 (when indeed a disastrous earthquake unfortunately happened). These results are in line with the fact that the model was trained on a corpus of news. On the other hand, the FinText model provides more disperse results. FinText is focused on financial language and related companies’ data, and indeed we see that e.g. the FTX collapse of November 2022 is well identified. “Russia” and “central banks” are also hinted as recurrent and meaningful centroids of information, but the instability and noise within outcomes is significant. For completeness, Fig. 3 shows the Principal Component Analysis (PCA) projection of points for sample dates 2023-02-26 and 2023-10-08, where the vectors come from the GoogleNews embeddings. The first two PCA components explain together ∼ 20% of the variance of the data, implying that the proposed representation must be interpreted with care. If we compare the centroids highlighted in Fig. 2 with the current plot, we anyways see some reasonable (despite noisy) structure identified. However, it is clear that the results can be unstable and have difficulties in unravelling deeper shades of information.
Overall, we conclude that the available pre-trained word embeddings allow us to generate an interesting (despite very basic) initial benchmark on expected central words for topics identification in the given time range. But as highlighted, many problems come with this methodology. We will soon proceed to introducing our novel graph-based methodology for narratives identification, which further allows us to assess whether a topic exists on its own, or is interconnected with other topics. However, we first briefly provide some meaningful remarks on the choices taken to account for the sentiment within our news.
4.2 Sentiment choice
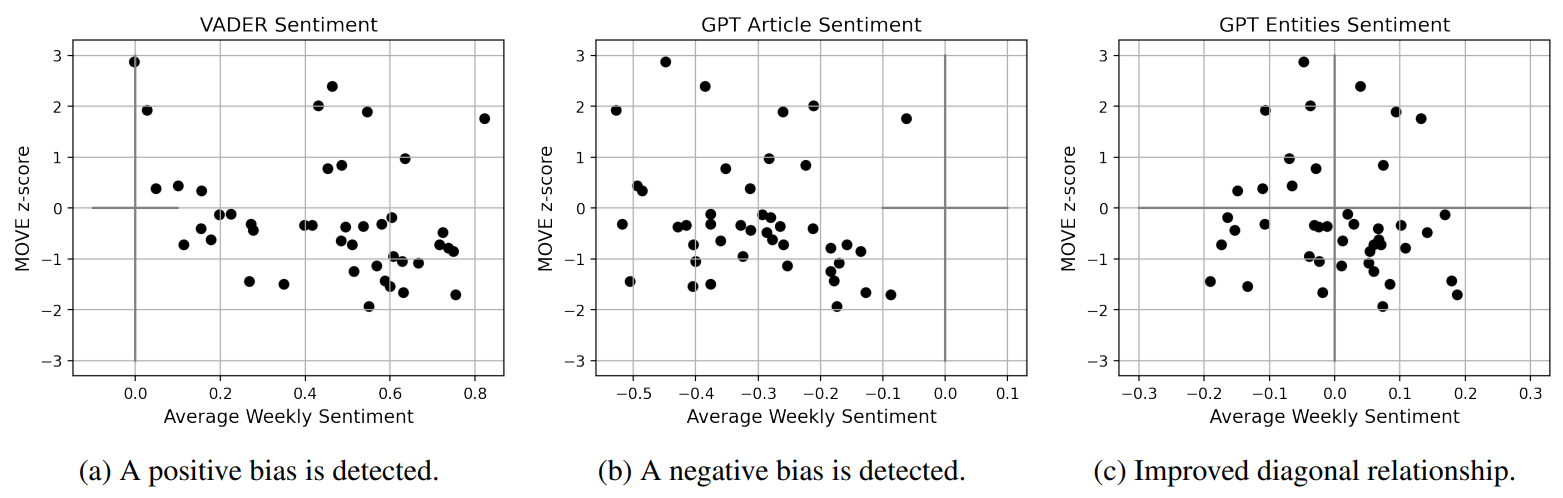
When analysing news, it is of clear importance to be able to accurately assess their related sentiment, especially if one desires to connect them to the state of financial markets. We believe that simply considering the overall sentiment of an article is restrictive, and decide to leverage on what GPT extracts as the sentiment surrounding the articles’ main entities. Thus, we provide now a brief motivating example that supports our approach.

4.3 Graph construction and initial measures
We can now proceed to introducing our novel graph-based methodology for narratives identification, which further allows us to assess whether a topic exists on its own, or is interconnected with other topics. As already hinted, the building blocks of our methodology are the ranked entities extracted by GPT from each article. For each week of news available, we thus generate a related representative graph G = (V, E) as follows:
1. The set of nodes V is constructed from the union of all entities extracted from the articles a ∈ A of the week. An attribute is also assigned to each node, which is the average of the (rank-weighted) sentiment extracted by GPT around such entity across articles.

4. Finally, we save the giant component of the graph.
For completeness to the above, we also show in Fig. 5 both the ratio of the size of the giant component versus the total initial number of nodes and the average clustering coefficient of the network, for each week. The latter is computed as the average among the local clustering coefficient for each node in the graph, which is the proportion of the number of links between a node’s neighbourhood divided by the number of links that could possibly exist between them.
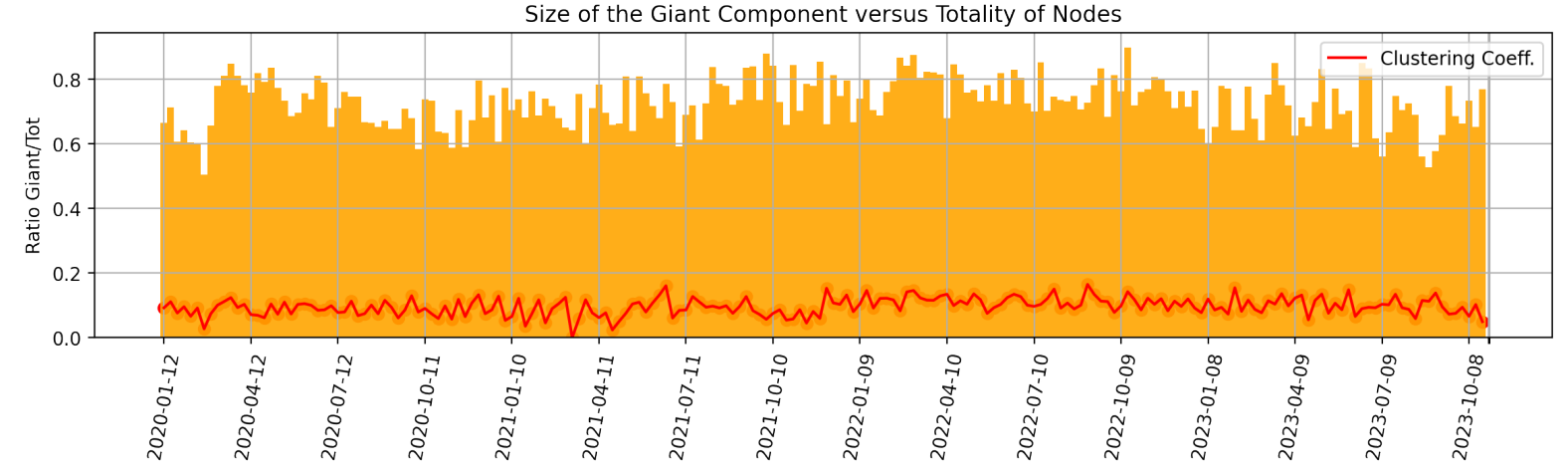
The giant components tends to encompass the large majority of the nodes (and be of size ∼ 200 − 300 nodes), meaning that we maintain significant amount of information, nevertheless with some intrinsic variability. When the second largest connected component has higher than average number of nodes, then it still tends to have only ∼ 20 − 30 nodes. For the sake of curiosity, we looked into a few such scenarios and report here an explicative example. For the week ending on 2022-12-04, the second largest connected component of the related graph is made of the following 21 nodes:
• sam bankman-fried, us bankruptcy courts, senate agriculture committee, john j ray iii, securities and exchange commission, cryptocurrency markets, alameda research, us trustee andrew vara, ftx, commodity futures trading commission, crypto lenders and hedge funds, valar ventures, us justice department, ledger x, blockfi, monsur hussain, sec and cftc, terrausd, newyork prosecutors and sec, three arrows capital, lehman brothers.
Clearly, this is a cluster of information related to the bankruptcy of the crypto exchange FTX in November, and its contagion to BlockFi Three Arrows Capital. However, this is disconnected from the giant component. Interestingly, we can thus inspect that e.g. the Securities and Exchange Commission (SEC) has no major other meaningful participation in the news, since otherwise the cluster would be connected to the giant component via that entity.
Thus, our approach allows us to focus on the interconnectedness of topics via the giant component of each graph, and to consequently try to extract the main narratives among weeks and their interrelations. Other “large” connected components can be considered to understand disconnected topics addressed in the news, but will not be of main relevance for the global state of the market. The average clustering coefficient of the giant component is then seen to simply oscillate around the value of 0.1, and thus does not provide strong direct insights. On the other hand, the degree and eigenvector centrality of nodes at different weeks will provide valuable information.
Centralities. We compute the weighted degree deg(v) and eigenvector centrality eig(v) for every node v in the giant component of the graph describing each week. Then, we focus on the three nodes with highest deg(v) and eig(v) for the given point in time, and show them in Figs. 6a and 6b, for the two measures respectively. In particular, we focus on entities that are recurrently important, i.e. we subset to entities that have highest centrality values for at least five weeks of our sample. For each week, we then plot the first, second, and third most important entities with the shape of a square, triangle, and cross, respectively. We size and annotate each point according to the actual value of the importance measure (rounded), and colour-code it according to the average sentiment around that entity. When we look at the nodes with highest degree, we are selecting the entities around which many news are focused. On the other hand, nodes with high eigenvector centrality are entities connected to other important entities, meaning entities lying at the center of the global net of interconnections among news.
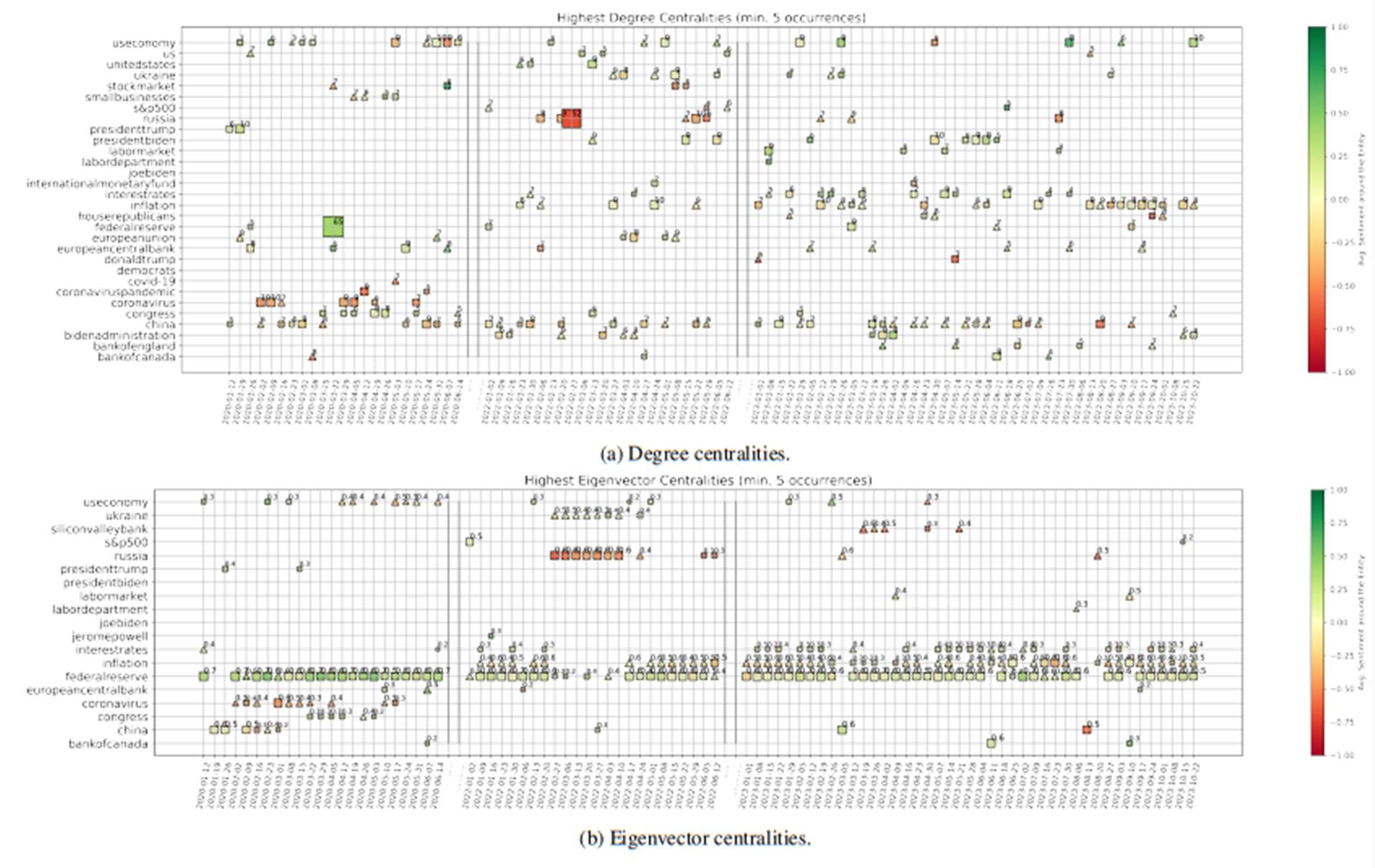
It is thus interesting to then analyse the different results arising from these two measures. We start from Fig. 6b, which shows snapshots of the evolution of nodes with highest eigenvector centrality. Clearly, the “Federal Reserve”, “inflation”, and “interest rates” play the major role in our net of news for the latest one year and a half. This is expected since such period is characterised by broad discussions about the persistently strong inflation, and the constant rate hikes of Central Banks. However, “Silicon Valley Bank” (SVB) also acquires significant importance at the end of March 2023, after it indeed collapsed on March 10th, 2023. The reason why this event has noteworthy eigenvector centrality (while it is not signalled by the degree centrality) is that SVB was the largest bank to fail since Washington Mutual closed its doors amid the financial crisis of 2008, on top of a moment of already strong fear of incoming recession in the U.S. Thus, such shock could have spread and affected current themes of discussion, meaning that our modelled interconnectedness of news was able to capture and highlight these broader concerns. Going further back in time, we see the strong concern around “Russia” and “Ukraine” at the beginning of 2022, when indeed the former invaded the latter. And clearly, “China” and the “Coronavirus” are signalled at the beginning of 2020, when the Covid-19 pandemic originated. Such entities are however not further signalled with the passing of time, meaning that the focus shifted on the consequences of such crisis rather than such topic itself.
We now move to the degree centralities shown in Fig. 6a. “Inflation”, and “interest rates” play again an important role, as expected. However, we have now more variability due to less interconnected topics but with high surrounding discussion. A negative shock related to “Russia” is clearly proposed in conjunction with the invasion of Ukraine, while a strongly positive one signals the pandemic stimulus approved by the Federal Reserve in March 2020. Interestingly, “China” appears quite constantly during our full sample of data, with e.g. a point of stronger negative sentiment and concern on the week ending on 2023-08-20. This is when Evergrande filed for U.S. bankruptcy protection as China economic fears mounted, while China also unexpectedly lowered several key interest rates earlier that week. Finally, we can further notice that “President Biden” and its Administration are some times highlighted, which is sensible due to the U.S. focus of our corpus. On top of that, data show indeed that e.g. “Donald Trump” carries strong negative sentiment the final weeks of 2022, when the January 6 committee decided he should indeed be charged with crimes related to the assault on the U.S. Capitol happened in 2021.
4.4 Community detection
The degree and eigenvector centralities of nodes in a graph can point to a concise sample of nodes of major interest, but they do not provide deeper insights on the structure and information within the totality of nodes. We believe that considering the problem of community detection on the proposed graphs will allow us to extract more insights on the topics characteristic of each week’s news, and on the evolution of the associated narratives. We slightly distinguish between the words “topic” and “narrative”, and consider the former as the broad category or label of a series of events, while the latter as the surrounding information that can evolve over time. As an example, we would refer to the “Covid pandemic” as a topic, while its narrative would evolve from the initial outbreaks, to the development of vaccines, to the posterior implications of the monetary policy adopted...

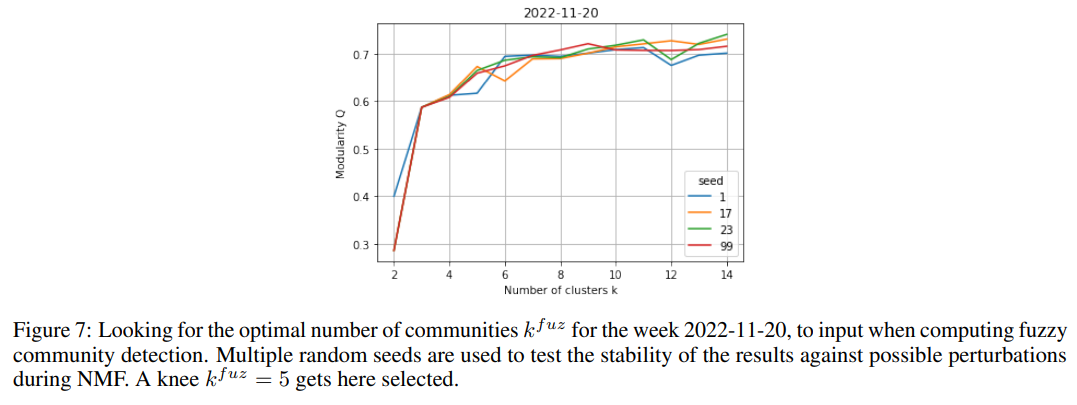
Importantly, we have been considering the strict partition generated by the introduced spectral method so far, but have not yet focused on its fuzziness component and stability of nodes. This is indeed leveraged upon now, since our hypothesis is that the communities highlighted by such method can be directly mapped to the main topics discussed within news. Thus, dropping the most unstable nodes will allow us to achieve a clearer and cleaner view. For each week, we proceed as follows:
-
For each community identified, we extract the list of nodes belonging to it.
-
For each related node i, we check whether Si ≤ 2 (i.e. if the level of membership in the most likely community is less than twice the level of membership to the second one). If the relationship is satisfied, then we label the node as unstable. Importantly, such threshold is chosen by looking at the distribution of stability indices over nodes for a sample of plots.
-
Then, we take all the news published that week. For each one node, we consider all articles for which the node is one of its five main entities. We further check whether all the three main entities of the article are in the nodes of the community under investigation, but not in the associated set of unstable nodes. The articles that satisfy all conditions are kept.
-
For each final set of articles representative of each community of the week, we save the related information (i.e. GPT-generated summary and GPT-generated abstract).
To summarise the above, we construct a set of highly representative articles for each community identified within the graph describing each week of data. We are very stringent with our stability requirements, and indeed drop on average 16 articles per community. However, this allows us to find the articles at the heart of each community, which enable the most effective downstream analyses. We then concatenate all related GPT summaries (and abstracts) for each community, and visualise them via word-clouds[5] to see whether they produce coherent topics. In parallel, we also feed such joint data into GPT and ask it to produce a newly associated summary, which should then allow us to easily interpret each topic (and narrative) of the week. The examples proposed in Fig. 8 aim to provide initial evidence of the accomplishments achieved by our methodology, where we show word-clouds of topics found for the weeks ending on 2022-01-23, 2022-11-20, and 2023-08-20. The related summaries of joint summaries are reported in Tables 1, 2, and 3, respectively, and we just mention that summaries on abstracts are highly similar. Importantly, we remark that if no articles belong to a community after our stability analyses, then clearly neither a word-cloud is shown nor a summary reported.
By studying the generated topics via word-clouds and proposed summaries, we find interpretable results that accurately map to the broad major events described by the data for each related week. Clusters for week 2022-11-20 are a nice example. On the other hand, we also see ability to extract the precursor worries of a Russian invasion of Ukraine from the findings of week 2022-01-23. This could be of great use for a thorough and systematic study of early signs of crises with more historical data. Moreover, one could compare the time of appearance of such signs across results computed

from different corpora, e.g. collected by news from Journals of different countries. Finally, we show the clusters for week 2023-08-20, since this is one of our latest occurrences of a market dislocation event (refer to Fig. 1). Interestingly, we see that many clusters are identified depicting concerns across themes of discussion. These different topics still need to be part of the giant component of our graph, implying that we have an instance of market turbulence related to high entropy of discussions within news that must be somehow more broadly interconnected.



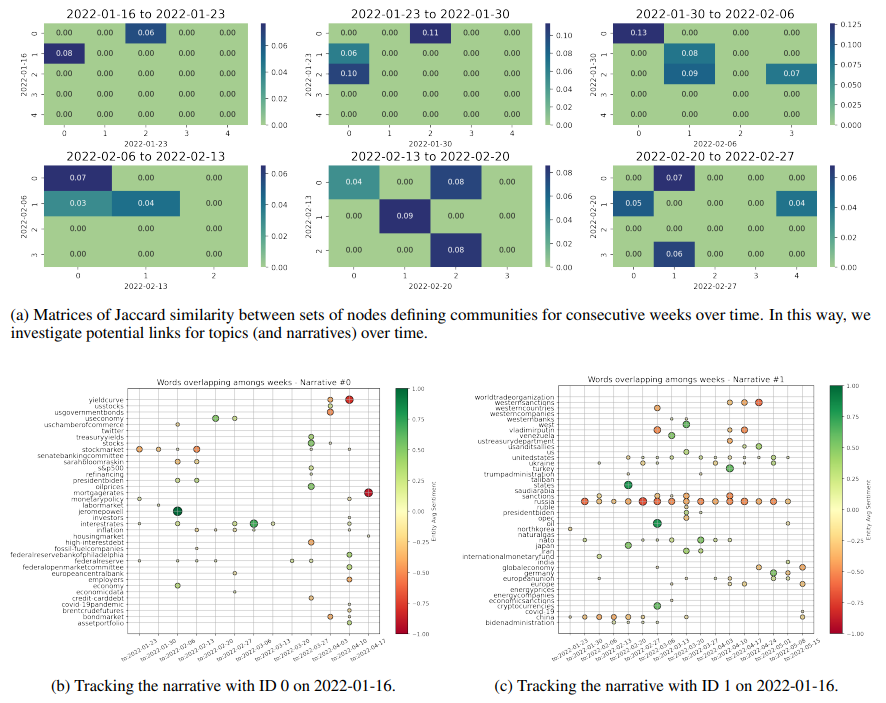
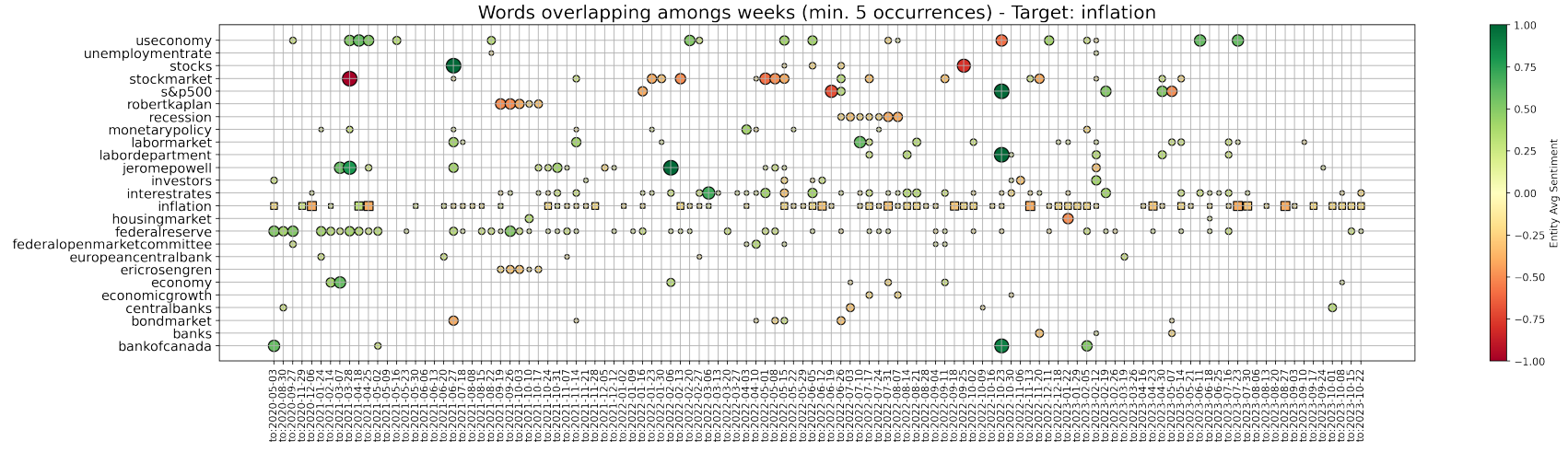
As an illustrative case, community 0 in Fig. 9a at week 2022-01-16 is most similar to community 2 at week 2022-01-23, which is then most similar to community 0 at week 2022-01-30, and the latter to community 0 again at week 2022-02-06, and so on. Of course, if no mapping is at some point found, then the narrative “has broken”. In Figures 9b and 9c, we respectively track both the shown topics 0 and 1 with the simple methodology proposed. We plot the nodes that are found to overlap for the most similar communities between each two consecutive weeks, until a mapping persists. It is direct to see that narrative 0 relates to inflation, interest rates, and the behaviour of Central Banks, while narrative 1 concerns Russia and the themes surrounding its war with Ukraine. In parallel, we also deploy a slightly different approach and just save the communities to which a chosen keyword belongs over time. In this way, we try to better investigate the surrounding evolving narrative. As an example, Fig. 10 shows the overlap of entities (generally plotted as dots) belonging to the same communities as the word “inflation” (plotted as squares) over consecutive weeks. New characters are highlighted, such as Eric Rosengren and Rober Kaplan, and an important period of concern is signalled around July 2022 and the word “recession”. Indeed, concerns about inflation, interest rates, and the fall of Gross Domestic Product (GDP) in the first two quarters of 2022, led to heightening recession fears during the month of July.
4.5 News and financial markets dislocations
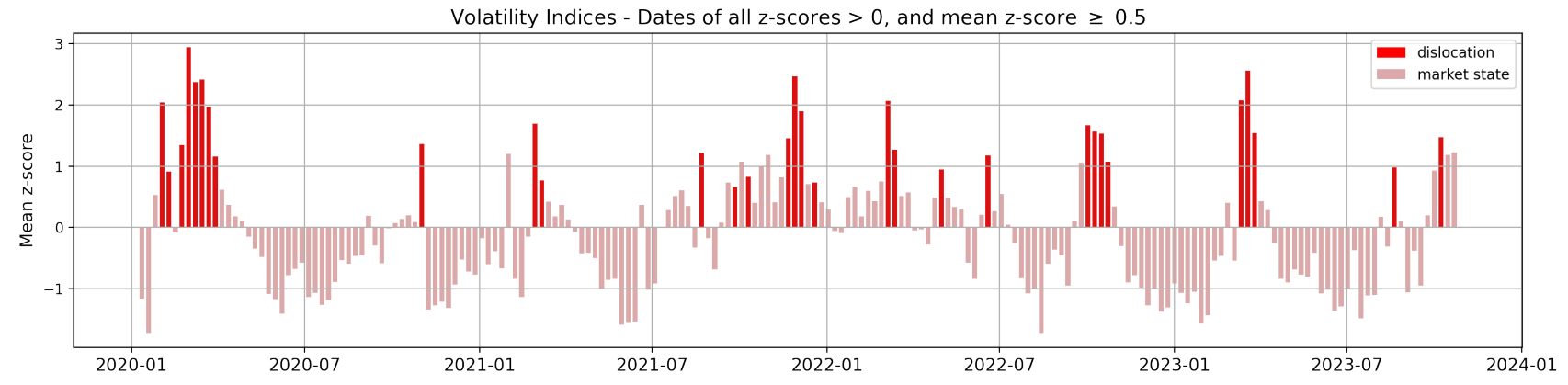
Thanks to the analyses just completed, we have supporting evidence on the ability of our graph constructs to advance in the task of topic detection and narrative characterisation. However, we now desire to test whether information on such structure of news allows us to unravel novel insights on broad market dislocations. As introduced in Section 2.2, we describe the state of the market by the z-scores of our volatility indices. Here, we then define a market dislocation as a week when all four of our z-scores are strictly positive, and their average is above 0.5. Such weeks are identified with a +1 label, while all other periods with a 0 label, implying that we now have a binary variable to use as target of a logistic regression model (see Section 3.4). For the sake of clarity, Fig. 11 shows our points of interest.
To run the suggested logistic regression, we need to build a set of features that characterise each week. Then, we can either map them to contemporaneous or next states of the market, to respectively investigate relationships between news and either unfolding or incoming dislocations. The features we consider can be seen to belong to three different categories, namely:
-
Market features. Features on the current state of the market (used in the case of predictive logistic regression, and as a benchmark). These are the current average of our four z-scores of volatility indices, and the difference of such value from the mean of the previous week.
-
News features. Features based on the raw corpus of news available.
-
Graph(+) features. Features extracted from the set of graphs that we built to capture the structure and interconnectedness of news within weeks. We further leverage on node2vec (n2v) embedding methodology.
Due to the limited number of data points (i.e. weeks) available, we build and test only features that we believe to be the most significant and meaningful for each category. Indeed, it is a common proxy to allow at least ∼ 20 outcomes for each independent variable tested. Also, we check the correlation among each pair of variables, to drop such features
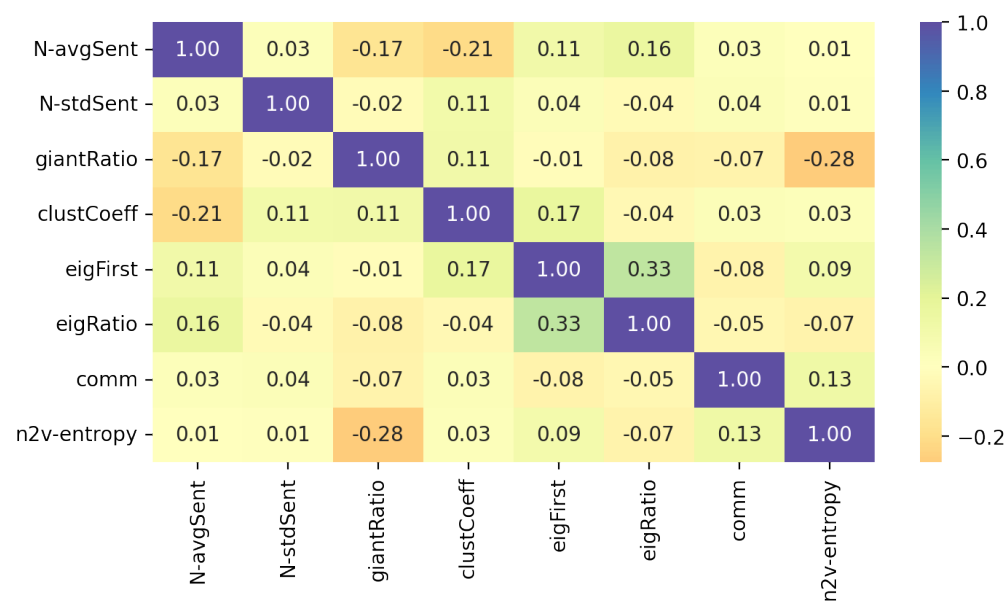
that would cause problems of multicollinearity and invalidate any results of the regression. Table 4 summarises our final set of 10 tested features and chosen related tags, while Fig. 12 shows their correlation matrix from Pearson’s test. As desired, all the retrieved features show either small or negligible correlation among each other.
Before proceeding to the logistic regression model itself, two points need to be now better discussed. These are the further features initially contrived but then dropped, and the methodology designed to construct the proposed “n2v-entropy” feature (i.e the last row in our table of features, with a “Graph+” class label). Our news features limit themselves to measures of the sentiment across articles, since we can safely assume that sentiment is indeed one of the most important market-related features that can be extracted from a plain corpus of economic news. We could have further included e.g. the specific number of news available for each week, but this would have been a noisy metric due to its strong dependence on the data collection step of our framework. Importantly, allowing for such simple but meaningful features of news gives us the opportunity to both test whether news have significant relationships with market dislocations, but also to assess whether our proposed graph representation of news is useful at all. Then, our graph features focus on characteristics that we can directly compute and extract from our graph representation of news in a week. For similar reasons as above, we do not include the absolute number of nodes and highest degree value of a graph (while we do compute the ratio between the size of the giant component and total number of nodes). Then, we do consider the average clustering coefficient of the network, but drop the average degree due to related high correlation. Due to a similar instance of high correlation, we unsurprisingly also drop the average and standard deviation of the sentiment of nodes in the graph. On the other hand, we retain the highest absolute value of nodes’ eigenvector centrality, and the ratio between such first and second highest values. The latter features allow us to better account for the structure of the network, and the potential presence of highly influential hubs. Finally, we also add to our set of features the optimal number of communities to partition the graph into, as identified by the fuzzy community detection methodology.

Regarding our graph+ feature, this is based on encoding nodes of each graph into an embedding space via the node2vec methodology (see Section 3.3). Node2vec has been shown to perform significantly well across a variety of practical tasks (such as mapping accuracy, greedy routing, and link prediction) on real-world graphs having from dozens to thousands of nodes [25]. It also suits us, since in this way we can design a metric that accounts for an holistic view of the topology of each graph. Importantly, node2vec embedding spaces cannot be compared across graph, meaning that we need to construct an ad-hoc downstream measure to characterise each point in time.
First of all, we begin by testing embeddings for multiple combinations of node2vec hyperparameters, in order to gauge the associated sensitivity of results. Similarly, we experiment with different combinations of the return parameter pemb and the in-out one qemb, in order to investigate the sampling strategy to adopt. Embeddings are thus computed for all (i.e. 24) the possible combinations of:

1. For each (orthogonal) dimension, we approximate the distribution of data on such axis by computing the probability of occurrence of points in bins of width 0.1.
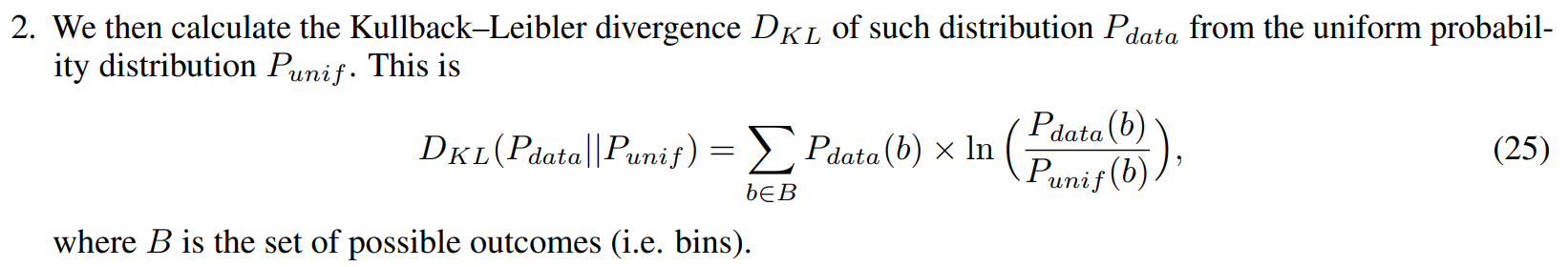
3. Finally, we average these divergences computed on our eight dimensions to achieve a proxy of global entropy. This is indeed named “n2v-entropy”.
Contemporaneous and predictive analyses. Now that we have introduced our target variable and motivated the features to test, we proceed to the implementation of our logistic regression models. Importantly, we consider data only from June 1st, 2020 to avoid dislocations related to the Covid-19 crisis. Such extreme exogenous shock would indeed prevent us to focus on more subtle and isolated moments of dislocations, which we believe to be the ones in need of better understanding. We also complete only in-sample tests, due to both the limited number of data points available and our specific interest on assessing whether useful information lies within the modelled structure and interconnectedness of news, on which one can then build upon if successfully proven. Since our dislocation dates are strongly under-sampled, we leverage on the SMOTE technique introduced in Section 3.4 to equally re-balance our target classes. We also standardise all features, and then train a logistic regression model for the following two cases:
-
We allow all features but market ones, and try to unravel connections between news and a contemporaneous state of market dislocation.
-
We allow all features, and try to predict an incoming state of market dislocation.
Despite prediction of incoming market dislocations is the most desirable end goal, we are indeed strongly interested in unravelling the features of news’ structure that are connected to such critical weeks. These would increase our understanding of such events with statistical confidence, and could suggest novel research ideas.
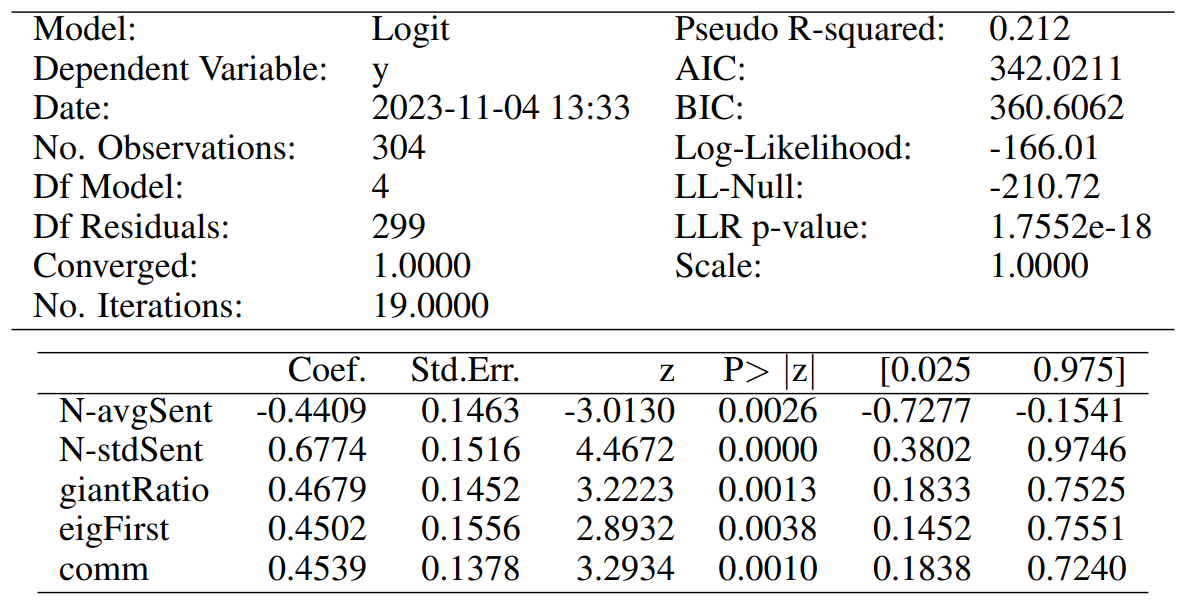
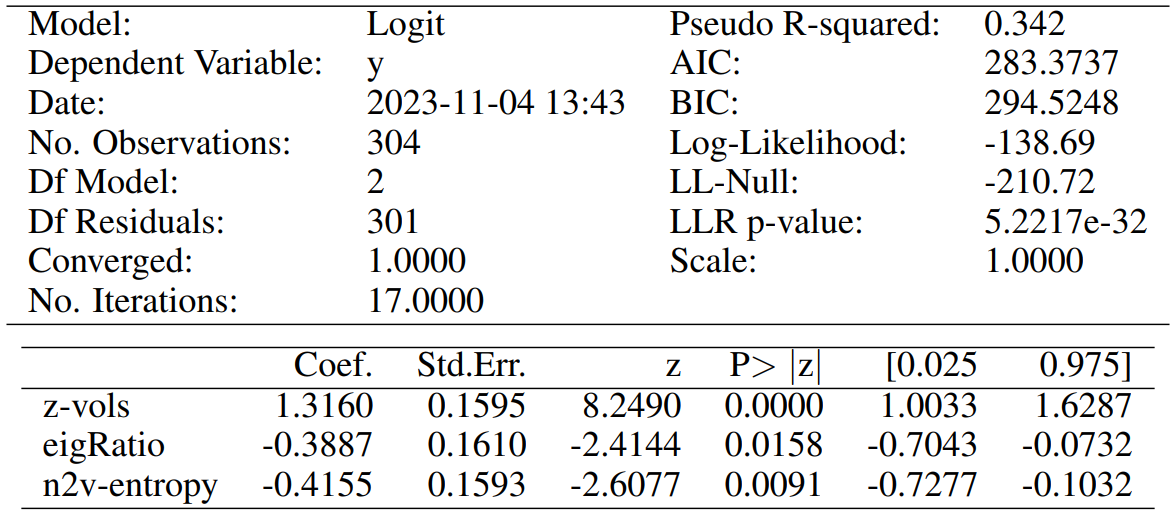
For each one of the two above cases, we do Recursive Feature Elimination (RFE) to complete feature selection, and require each chosen attribute to be significant at least at the p-value < 0.05 level. The full specifications of our final models are reported in Tables 5 and 7, for our contemporaneous and predictive cases, respectively. Similarly, Tables 6 and 8 report the associated confusion matrices on their left, which arise from testing back our resultant models on the (not over-sampled) initial data. The latter tables also report a few further metrics on their right. Indeed, we show the precision of our classifier, which is its ability to not label a sample as positive if it is negative (i.e. the ratio between true positives divided by the sum of true positives and false positives). Then, the recall assesses the ability of the classifier to find all the positive samples (and is computed as the ratio between true positives divided by the sum of true positives and false negatives). Finally, the F-beta score can be interpreted as a weighted harmonic mean of the precision and recall, and reaches its best value at 1 and worst score at 0.
Our model for the contemporaneous relationship between news and market dislocations proposes five significant features. Both the average and standard deviation of simple news’ sentiment (i.e. “N-avgSent” and “N-stdSent”) are among them, with the former having unsurprisingly negative coefficient. Thus, a more positive sentiment of news clearly lowers the probabilities of being in a moment of market dislocation. We also believe that a higher standard deviation generally implies a subset of articles with stronger negative sentiment rather than positive, and thus a positive coefficient is seen. The “giantRatio”, “eigFirst”, and “comm” features are instead related to our proposed graph characterisation of weekly news, and have all positive coefficient. Having a larger proportion of nodes kept within each graph’s giant component implies that articles are more interconnected within each other, but a higher number of communities suggests that there are also more themes of discussion. Then, a larger first eigenvector centrality value suggests very influential hubs (i.e. concepts) within the construct. Merging all such information, we can see that the model hints to a relationship between market dislocations and high entropy of discussion among news. The latter need anyways to be in some way interconnected by construction, and thus point to contagion effects among themes of concern.
On the other hand, our model to predict incoming market dislocations proposes only three significant features. Clearly, the current state of the market is the strongest predictor for possible dislocations, but both “eigRatio” and “n2v-entropy” are still found significant and with not-negligible participation in the definition of the outcome probability. Such attributes have coefficients with negative sign, for which we now propose a motivation. A lower ratio between the first and second eigenvector centralities implies that the two related nodes have importance values more similar in magnitude. Thus, this refers to a situation in which there are competing hubs of importance, and likely competing points of concerns. Similarly, a lower Kullback-Leibler divergence actually implies higher entropy within the generated node2vec nodes’ embeddings. Such higher entropy points to less uniform structure within narratives, which seems to indeed encode an early alert of incoming market dislocations.
Despite being very simple initial analyses, the considerations just outlined provide a baseline of evidence for a connection between news structure (i.e. beyond their mere sentiment) and market dislocations. Therefore, these first results further motivate the analyses proposed at the beginning of this project, and should prompt more studies that leverage on our graph construct to investigate broad corpora of news.
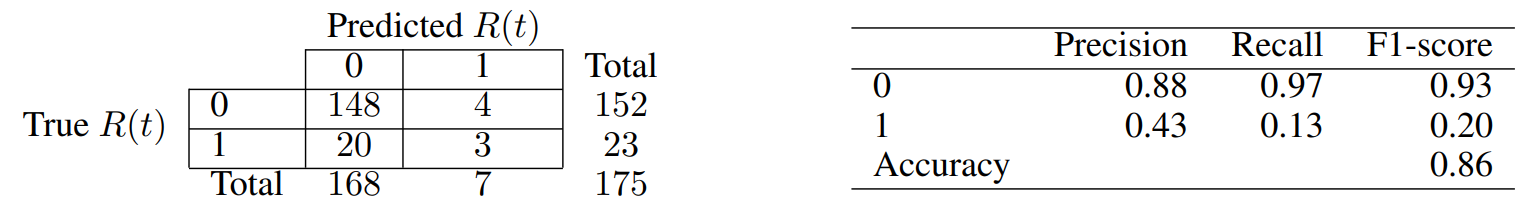
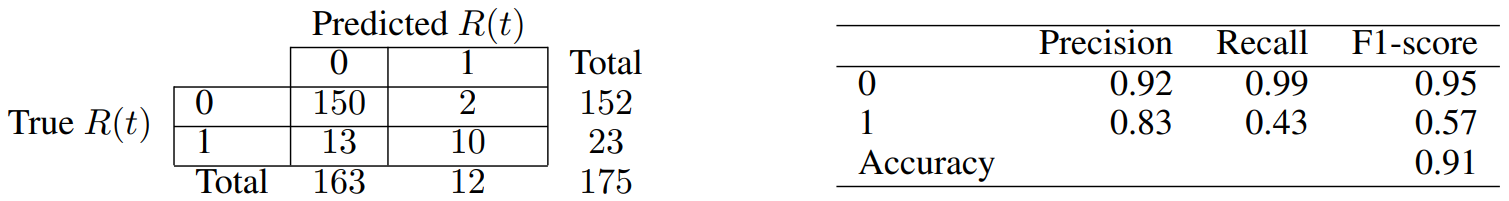
This paper is available on arxiv under CC0 1.0 DEED license.
[5] A word-cloud is a collection of words depicted in different sizes and strengths to indicate the frequency and importance of such word in the text.