Authors:
(1) Troisemaine Colin, Department of Computer Science, IMT Atlantique, Brest, France., and Orange Labs, Lannion, France;
(2) Reiffers-Masson Alexandre, Department of Computer Science, IMT Atlantique, Brest, France.;
(3) Gosselin Stephane, Orange Labs, Lannion, France;
(4) Lemaire Vincent, Orange Labs, Lannion, France;
(5) Vaton Sandrine, Department of Computer Science, IMT Atlantique, Brest, France.
Table of Links
Estimating the number of novel classes
Appendix A: Additional result metrics
Appendix C: Cluster Validity Indices numerical results
Appendix D: NCD k-means centroids convergence study
7 Experiments
7.1 Experimental setup
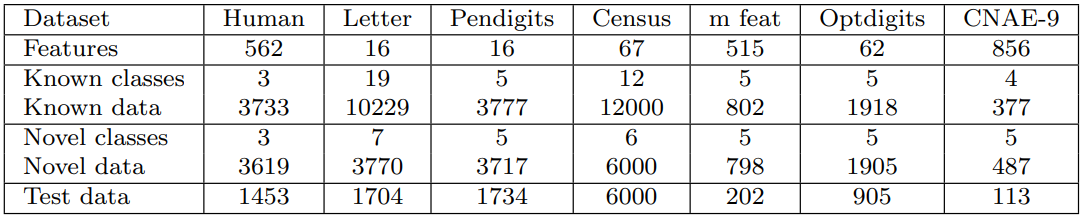
Datasets. To evaluate the performance of the methods compared in this paper, 7 tabular classification datasets were selected: Human Activity Recognition [35], Letter Recognition [36], Pen-Based Handwritten Digits [37], 1990 US Census Data [37], Multiple Features [37], Handwritten Digits [37] and CNAE-9 [37].

Metrics. We report the clustering accuracy (ACC) on the unlabeled data. It is defined as:

Competitors. We report the performance of k-means and Spectral Clustering, along with their NCD-adapted versions introduced in Sections 3.2 and 3.3. We also include PBN and the pioneering NCD work for tabular data, TabularNCD [9]. Finally, we implement the same baseline used in [9]. It is a simple deep classifier that is first trained to distinguish the known classes. Then, the penultimate layer is used to project the data of the novel classes before clustering it with k-means. See the discussion of Section 3.4 for more details. We will call this approach the “baseline” for the remainder of this article.
Implementation details. The neural-network based methods (i.e. PBN, TabularNCD and the baseline) are trained with the same architecture: an encoder of 2 hidden layers of decreasing size, and a final layer for the latent space whose dimension is optimized as an hyperparameter. The dropout probability and learning rate are also hyperparameters to be optimized. The classification networks are all a single linear layer followed by a softmax layer. All methods are trained for 200 epochs and with a fixed batch size of 512. For a fair comparison, the hyperparameters of these neuralnetwork based methods are optimized following the process described in Section 4 (whereas the parameters of NCD SC are simply optimized following Section 3.3). Thus, the labels of the novel classes are never used except for the computation of the evaluation metrics reported in the result tables. The hyperparameters are optimized by maximizing the ARI, and their values can be found in Annex B.
7.2 Results analysis
7.2.1 Results when the number of novel classes is known in advance

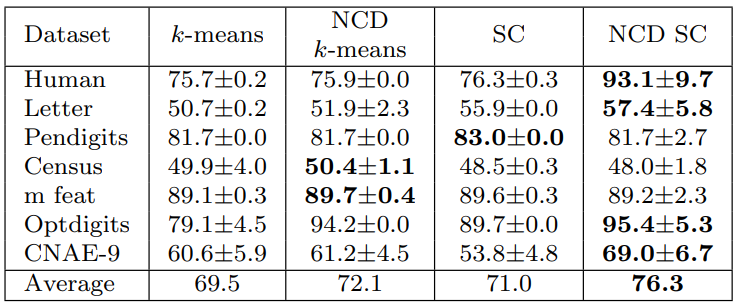
The comparison between NCD k-means and NCD SC confirms the idea that no single clustering algorithm is universally better than the others in all scenarios, as noted by [39]. However, NCD SC outperforms its competitors on 4 occasions and has a the highest average accuracy. Therefore, this algorithm is selected for the next step of comparisons.
NCD. As shown in Table 4, PBN outperforms both the baseline and TabularNCD by an average of 21.6% and 12.9%, respectively. It is only outperformed by the baseline on the Letter Recognition [36] dataset. This dataset consists of primitive numeric attributes describing the 26 capital letters in the English alphabet, which suggests a high feature correlation between the features used to distinguish the known and novel classes. Since the baseline learns a latent space that is strongly discriminative for the known classes, this gives the baseline model a distinct advantage in this specific context. On the other hand, we observe that it is at a disadvantage when the datasets do not share as many high-level features between the known and novel classes.
Table 4 also demonstrates the remarkable competitiveness of the NCD Spectral Clustering method, despite its low complexity. On average, it trails behind PBN by only 1.0% in ACC and manages to outperform PBN twice over 7 datasets.
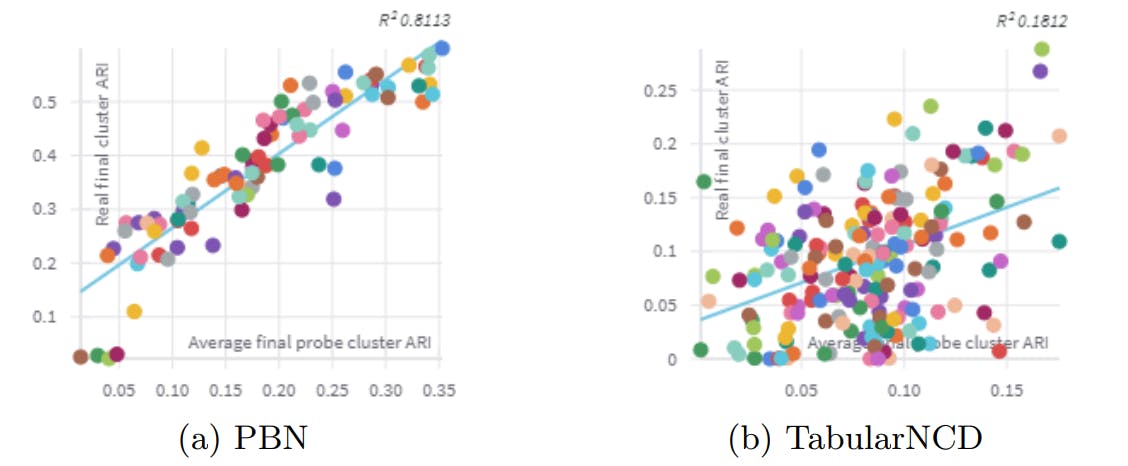
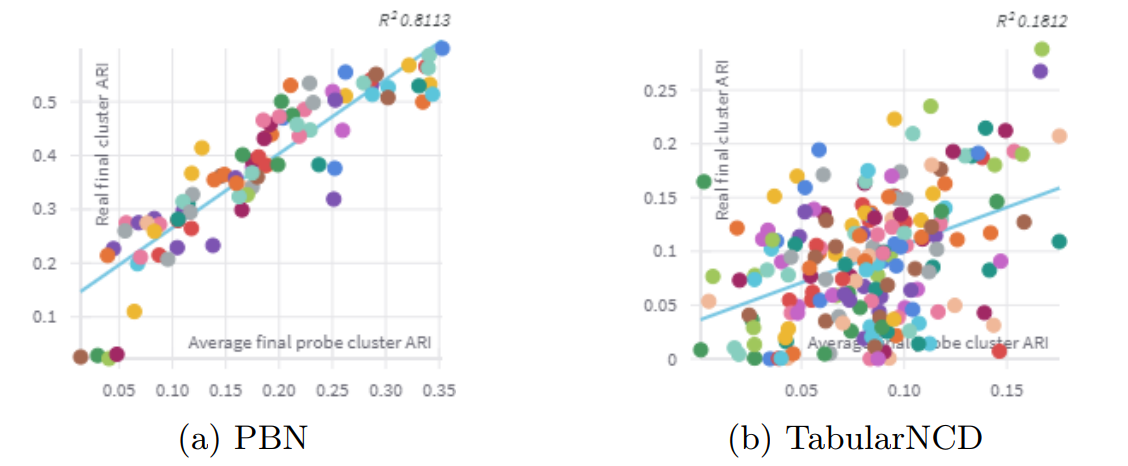
To investigate the reasons behind the subpar performance of TabularNCD, we look at the correlation between the ARI on the hidden classes and the final ARI of the model on the novel classes. A strong correlation would imply that if a combination of hyperparameters performed well on the hidden classes, it would also perform well on the novel classes. To examine this, we plot the average ARI on the hidden classes against the ARI on the novel classes. Figure 5 is an example of such a plot. It shows that, in the case of the Letter Recognition dataset, PBN has a much stronger correlation than TabularNCD. We attribute this difference to the large number of hyperparameters of TabularNCD (7, against 4 for PBN), which causes the method to overfit on the hidden classes, resulting in a lack of effective transfer of hyperparameters to the novel classes.

7.2.2 Results when the number of novel classes is estimated
As expressed in Section 5, we leverage the representation learned by PBN during the k-fold CV to estimate the number of clusters. The result is a method that never relies on any kind of knowledge from the novel classes. This approach is also applicable to the baseline and the spectral embedding of SC, but not to TabularNCD as it requires a number of clusters to be defined during the training of its representation. For a fair comparison, TabularNCD is trained here with a number of clusters that was estimated beforehand with a CVI.

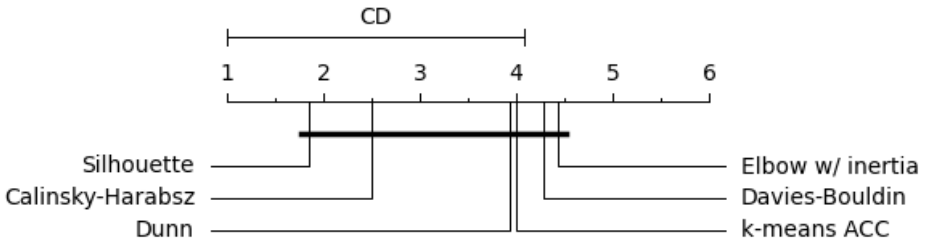
Nevertheless, we find that the Silhouette coefficient performed the best in the latent space of PBN, closely followed by the Calinski-Harabasz index. The elbow method is ranked last, which could be explained by the difficulty in defining an elbow [2].

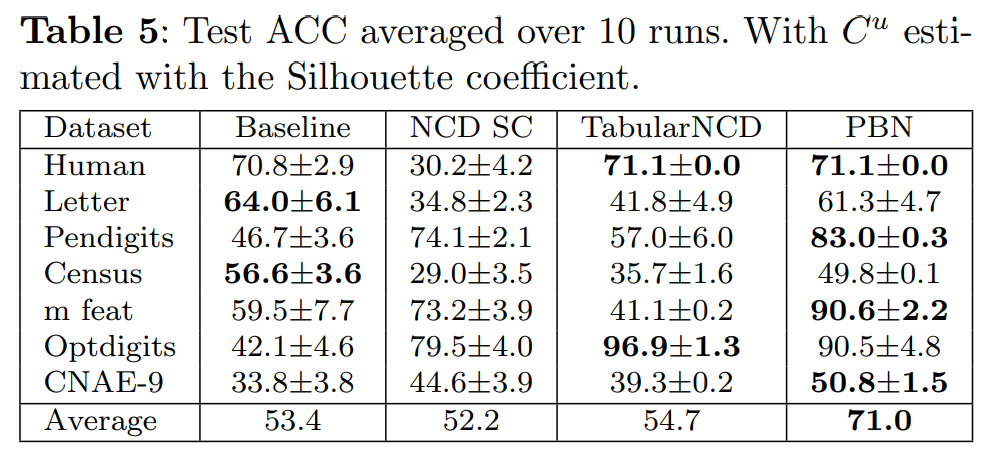
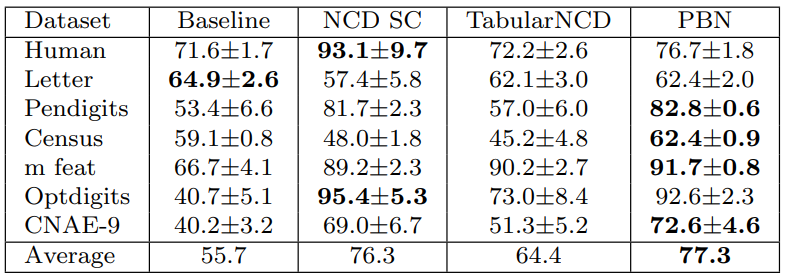
As emphasised earlier, Table 5 reports the results of the different NCD algorithms in the most realistic scenario possible, where both the labels and the number of novel classes are not known in advance. This is the setting where PBN exhibits the greatest improvement in performance compared to the other competitors, achieving an ACC that is 17.6%, 18.8% and 16.3% higher than the baseline, NCD SC, and TabularNCD, respectively.

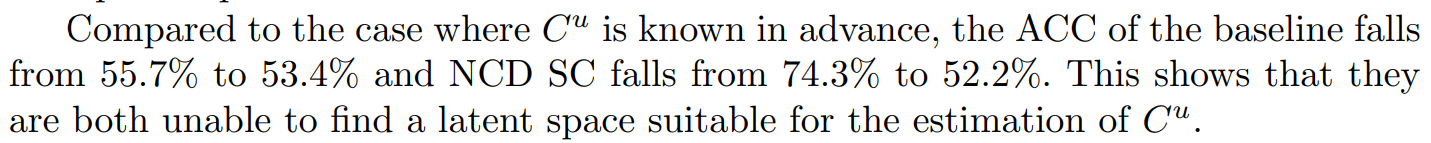
However, the ACC of PBN remains an impressive 71.0%, demonstrating that this simple method, comprising of only two loss terms, is the most appropriate for tackling the NCD problem in a realistic scenario. In contrast to the baseline and NCD SC methods, its reconstruction term enables it find a latent space where the unlabeled data are correctly represented. And unlike TabularNCD, it has a low number of hyperparameters which decreases the probability of overfitting on the hidden classes during the k-fold CV procedure.
This paper is available on arxiv under CC 4.0 license.
[2] There are no widely accepted approaches, as the concept of an “elbow” is subjective. In this study, we employed the kneedle algorithm [40] through the kneed Python Library [41].