Authors:
(1) Wahei Hara;
(2) Yuki Hirano.
Table of Links
- Abstract and Intro
- Exchanges and Mutations of modifying modules
- Quasi-symmetric representation and GIT quotient
- Main results
- Applications to Calabi-Yau complete intersections
- Appendix A. Matrix factorizations
- Appendix B. List of Notation
- References
4. Main results
4.1. Wall crossing and tilting equivalence. This section shows that wall-crossings of magic windows correspond to equivalences that are induced by tilting modules.


Proof. By Teleman’s quantization theorem [Tel], for all k ∈ Z, the natural restriction map induces an isomorphism



of equivalences is commutative.
Proof. (1) The adjunction gives an isomorphism

Therefore we only need to prove that the right hand sides of (4.E) and (4.F) are isomorphic functors. But this follows from a natural isomorphism



Lemma 4.8. Notation is same as above.

(2) This also follows from Lemma 3.19 and the fact that µδ,δ′ is a bijection.
(3) This is a consequence of (2).
For each F ∈ F(δ,δ′)
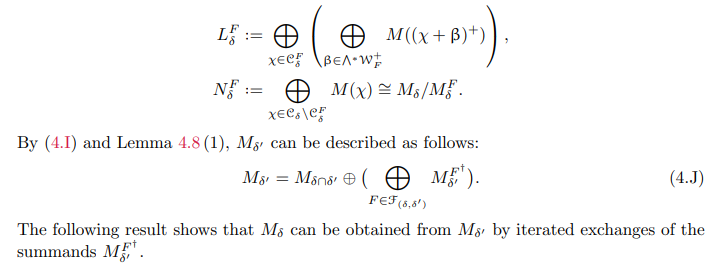
Theorem 4.9. Notation is same as above.
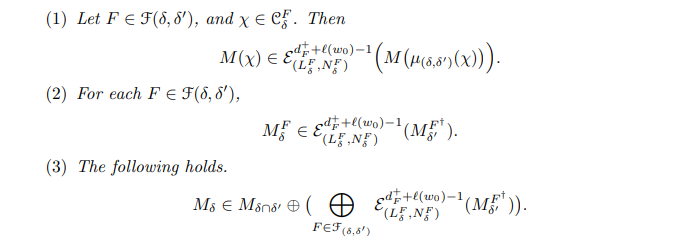
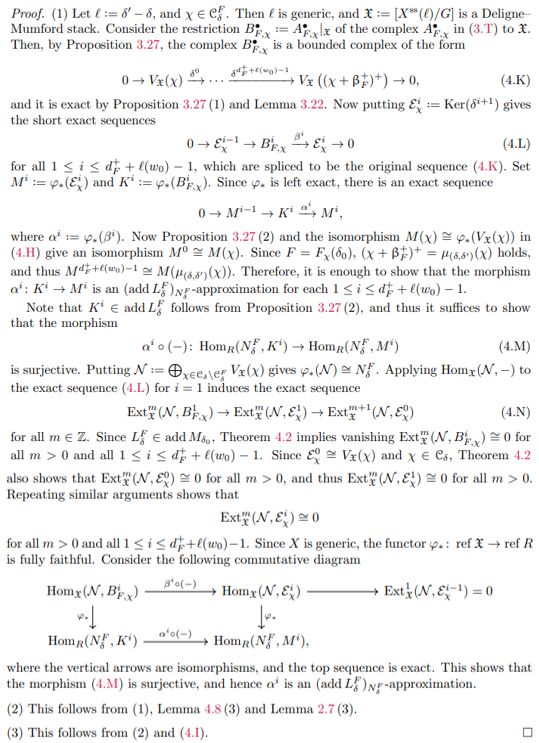



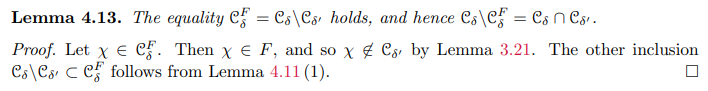








This paper is available on arxiv under CC0 1.0 DEED license.

