Author:
(1) Hiroki Takizawa, Preferred Networks, Inc., Chiyoda-ku, Tokyo, Japan (contact@hiroki-takizawa.name).
Table of Links
Discussion and Conclusions and Acknowledgements
Additional Information and Declarations and References
4 Results
First of all, we enumerated and shortly evaluated all positions with 50 empty squares. We only enumerated positions with at least one legal move and considered symmetrical positions to be identical. As a result, 2,958,551 positions were enumerated. We evaluated all of them by Edax for 10 seconds using a single CPU core. For positions that resulted in values close to a draw from the 10-second evaluations, we conducted more extended evaluations.
Next, we selected 2,587 positions out of the 2,958,551 positions and formulated hypotheses regarding their game-theoretic values. We chose them such that if all these hypotheses were proven correct, it would prove that the initial position results in a draw. Although there are numerous ways to select subsets that would prove that the initial position results in a draw, we used Algorithm 1 to obtain a small subset. For the evaluation values, we used the values obtained from the previously mentioned evaluations.
In cases where the values were the same, we prioritized positions that appear frequently in the WTHOR database[23] of Othello games published by the French Othello Federation. We used a dataset including 61,549 game records played between 2001 and 2020. As we will describe in detail later, it was proven that all these 2,587 hypotheses were correct.
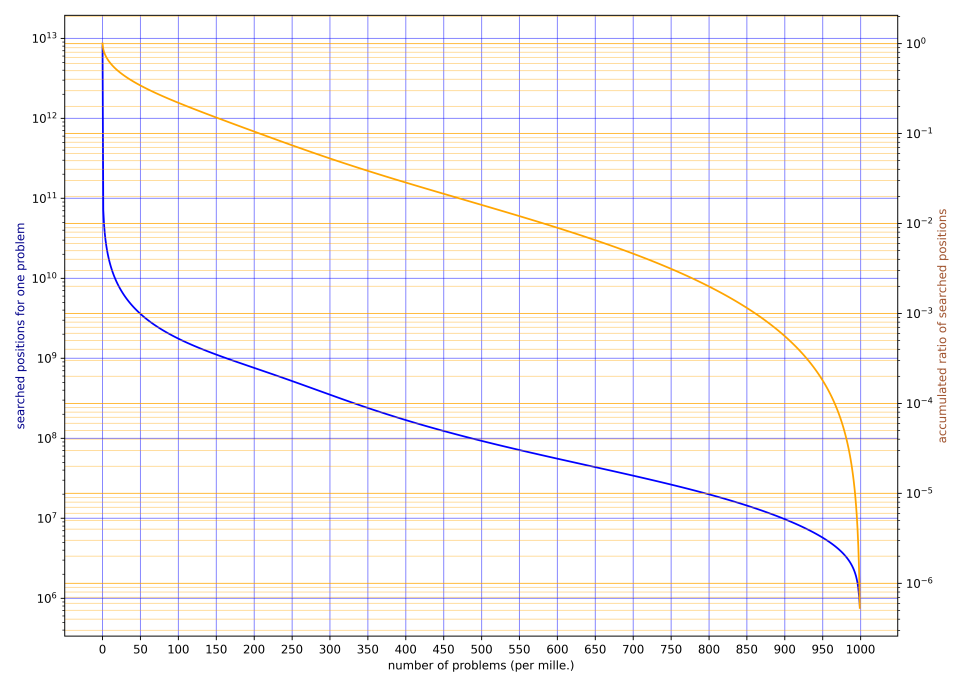
As a result, the number of positions with 36 empty squares needed to solve the initial position amounted to 1, 505, 367, 525, with the total search positions reported by Edax for all these positions reaching 1, 526, 001, 455, 595, 489, 506 (Figure 2, Table 1). Due to having the alpha-beta window set to [−3, +3] for some borderline positions, there seems to be room for reduction in this number. As a null-window search is available for verification, the number of necessary search positions could potentially be even lower.
The results of the opening are illustrated in Figure 4. Our perfect player never voluntarily deviates from the optimal game record (shown as bold black moves). If the opponent chooses a move not shown in this figure, we proved that our

player will always win. If the opponent chooses one of the non-bold moves, we proved that our player draws or wins by choosing moves shown as bold gray moves.
This paper is available on arxiv under CC 4.0 license.

