Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
2. Notation and outline of the proof
Notation and conventions.
Throughout, t, u, v, z and σ denote real variables; x and y denote positive real variables; s and w denote the complex variables s = σ +it and w = u+iv; d, h, j, k, l, m, n and r denote natural numbers, while p and q denote primes; the arithmetic functions µ(n) and ϕ(n) are defined as usual, while τk(n) denotes the k-fold divisor function. Let ∗ denote the Dirichlet convolution of arithmetic functions. Let e(s) = exp{2πis}. We write

We let χ denote a real primitive character to the modulus D with D greater than a sufficiently large and effectively computable number. Write
L = log D. (2.1)
Let c denote a positive, effectively computable and absolute constant, not necessarily the same at each occurrence. All implied constants, unless specified, are absolute and effectively computable. In this paper, an error term is usually given in the form that is small enough for our purpose, although shaper estimates are possible.
For any Dirichlet character θ to the modulus k, let τ (θ) denote the Gauss sum
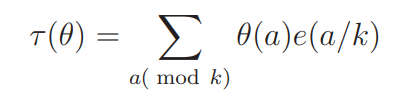
(thus we shall not write τ for τ2, the ordinary divisor function). The expressions
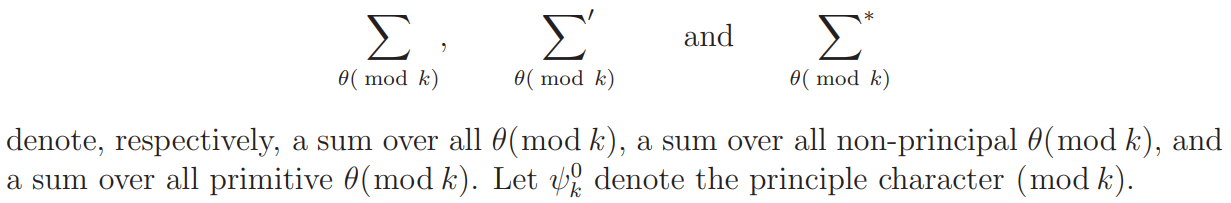
In case θ(mod k) is a primitive character, the functional equation for L(s, θ) is
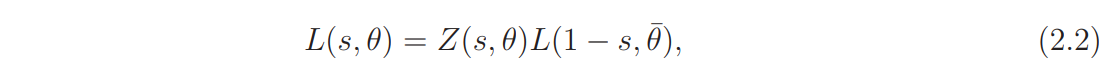
where
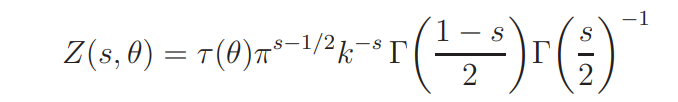
if θ(−1) = 1, and
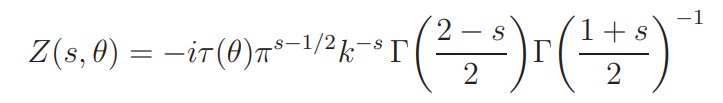
if θ(−1) = −1. When t is large, it is convenient to use an asymptotic expression for Z(s, θ) as follows. Let
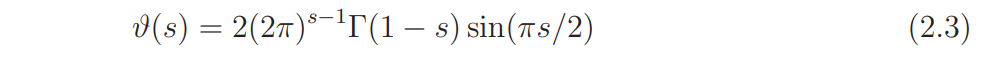
(this function is usually written as χ(s) in the literature). It is known that
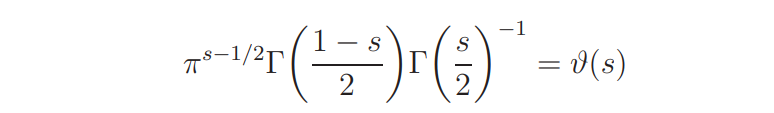
and
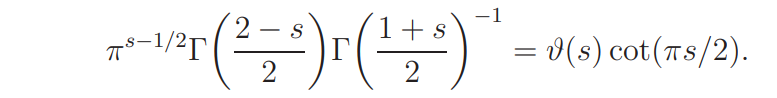
Assume t > 1. Then
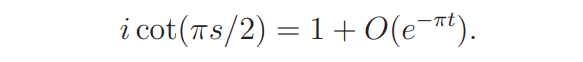
Thus we have uniformly
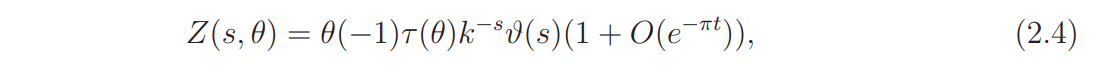
and
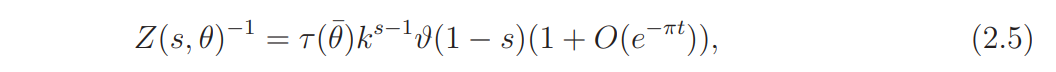

Outline of the proof: Initial steps
Our aim is to derive a contradiction from the following
Assumption (A)
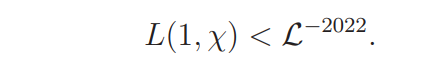
The underlying ideas are inspired by the work of Goldfeld [10], Iwaniec and Sarnak [15] and Conrey, Ghosh and Gonek [4]. The paper [10] exhibits a relationship between the lower bound for L(1, χ) and the order of zeros of the function LE(s)LE(s, χ) at the central point, where E is an elliptic curve; the paper [15] exhibits a relationship between the lower bound for L(1, χ) and the non-vanishing of central values of a family of automorphic L-functions; the paper [4] has definite influence on the idea of reducing the problem to evaluating certain discrete means that is employed in the present work (the reader is also referred to [3]).
The initial part of this paper consists in relating the lower bound for L(1, χ) to the distribution of zeros of the function L(s, ψ)L(s, ψχ), with ψ belonging to a large set Ψ of primitive characters, in a domain Ω. Thus we introduce

For notational simplicity we write
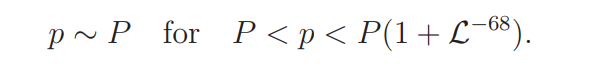
Let Ψ be the set of all primitive characters ψ(mod p) with p ∼ P, and let
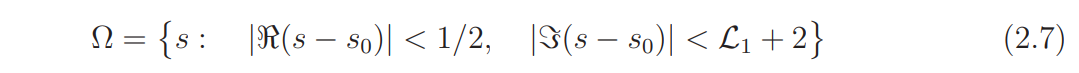
where
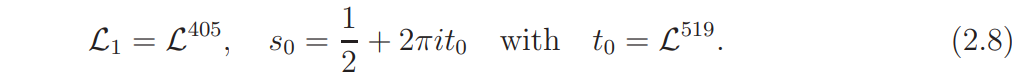
Throughout, we will assume that p ∼ P and ψ is a primitive characters (mod p), i.e., ψ ∈ Ψ. Note that
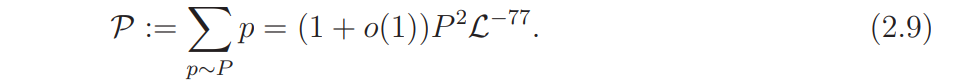
In Section 3 we shall introduce a subset Ψ1 of Ψ and prove
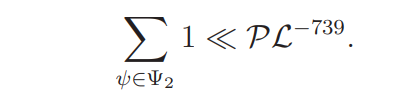
For ψ(mod p) ∈ Ψ, the average gap between consecutive zeros of L(s, ψ)L(s, ψχ) in Ω is
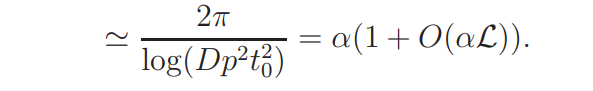
where

In Section 4 we shall prove
Proposition 2.2. Suppose that ψ ∈ Ψ1. Then the following hold.
(i). All the zeros of L(s, ψ)L(s, ψχ) in Ω lie on the critical line.
(ii). All the zeros of L(s, ψ)L(s, ψχ) in Ω are simple.
(iii). The gap between any consecutive zeros of L(s, ψ)L(s, ψχ) in Ω is of the form
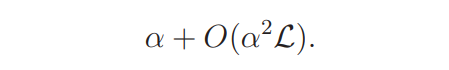
It should be stressed that the set Ψ1 is formally defined. In fact, Proposition 2.2 and some other results for ψ ∈ Ψ1 are unconditionally derived from the definition of Ψ1.
However, one is even unable to determine whether Ψ1 is empty or not without assuming (A).
The results of Proposition 2.1 and 2.2 are not surprising and they go back to HeathBrown [15]. One may believe that the assertions (i) and (ii) of Proposition 2.2 hold for all characters ψ in Ψ. On the other hand, however, in comparison with some conjectures on the vertical distribution of zeros of the Riemann zeta function (see [2] and [17]), one may claim that the gap assertion (iii) of Proposition 2.2 fails to hold for most of ψ in Ψ. Our proof thus consists in deriving a contradiction from the gap assertion.
Assume ψ ∈ Ψ. Recall that the functional equation for L(s, ψ) is given by (2.2) with θ = ψ. On the upper-half plane, since Z(s, ψ) is analytic and non-vanishing, there is an analytic function Y (s, ψ) such that
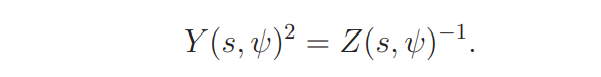
Let
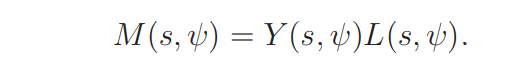
Note that M(s, ψ) is defined for t > 0 only, and, for each ψ, there are two choices of M(s, ψ) up to ±, but the expressions
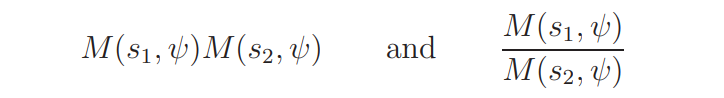
are independent of these choices. The functional equation (2.2) gives
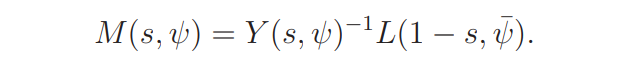
Since |Y (1/2 + it, ψ)| = 1, it follows that
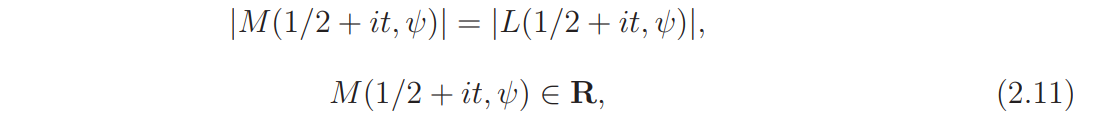
and, consequently,
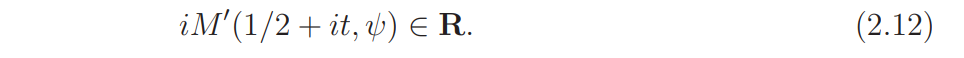
The gap assertion (iii) of Proposition 2.2 can be restated as follows. If ψ ∈ Ψ1 and (1/2 + iγ, 1/2 + iγ′ ) is a pair of consecutive zeros of L(s, ψ)L(s, χψ) in Ω with γ ′ > γ, then for some (large) constant c ′ > 0,
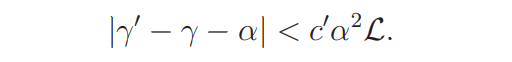
Write
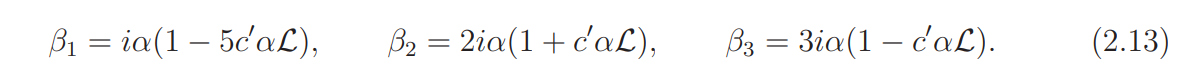
In what follows we assume ψ ∈ Ψ1. Let Z(ψ) denote the set of zeros of L(s, ψ) in the region
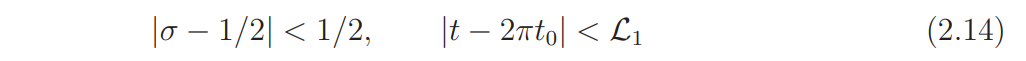
(this is slightly smaller than Ω). Assume ρ ∈ Z(ψ). Note that
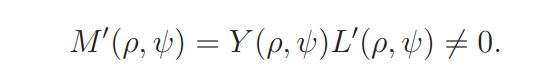
Write
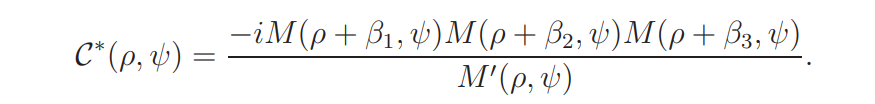
By (2.11) and (2.12) we have
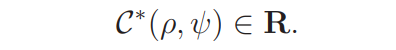
It will be proved that
Lemma 2.3. Suppose ψ ∈ Ψ1 and ρ ∈ Z(ψ). Then
C ∗ (ρ, ψ) ≥ 0.
We introduce the smooth weight
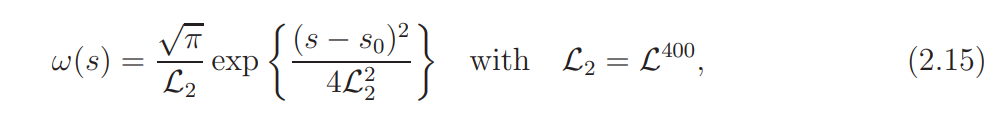
which is positive for σ = 1/2. Lemma 2.3 implies that
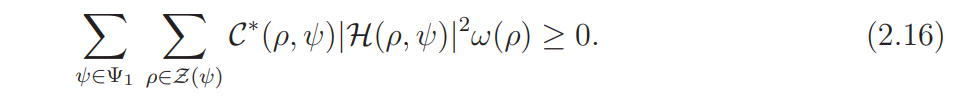
for all functions H(s, ψ) defined on Ω. Thus, in order to derive a contradiction from (A), it suffices to find certain functions H(s, ψ) and show that , under Assumption (A), (2.16) fails to hold.
A heuristic argument
It is natural to consider the function H(s, ψ) which is of the form
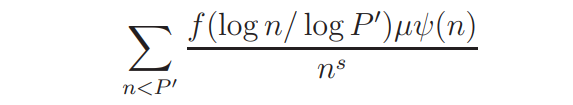
for some P ′ < P, where f is a polynomial with f(1) = 0. It should be stressed, on assuming (A), that if H(s, ψ) is of the above form with P ′ slightly smaller than P in the logarithmic scale, the sum in (2.16) can be evaluated. This is analogous to the results of Conrey, Iwaniec and Soundararajan [5] and [6]. However, it seems that such a choice of H(s, ψ) is not good enough for our purpose. On the other hand, the left side of (2.16) could be “close” to zero for certain non-zero functions H(s, ψ). For example, one may consider the choice that H(s, ψ) is a linear combination of L(s+βj , χψ), 1 ≤ j ≤ 3. Thus, inspired by the approximate formula for L(s, χψ), some new forms of H(s, ψ) could be introduced. However, our goal is not to show that (2.16) fails to hold for certain H(s, ψ) directly, instead, a variant of the argument will be adopted.
The crucial part of the proof is to construct functions H1(s, ψ), H2(s, ψ), J1(s, ψ) and J2(s, ψ), each of which is of the form
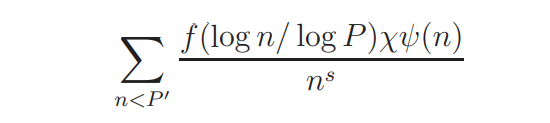
with log P ′/ log P close to 1/2, and show that the left side of (2.16) is ”small” if
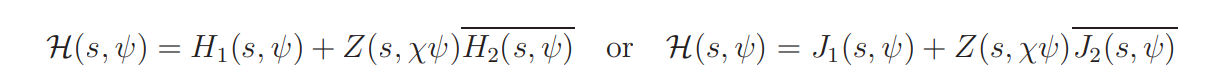
for σ = 1/2. On the other hand, the sum
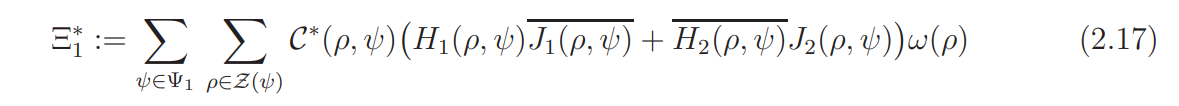
is not too small in absolute value.

Discrete mean estimates
We introduce some parameters and functions as follows. Let
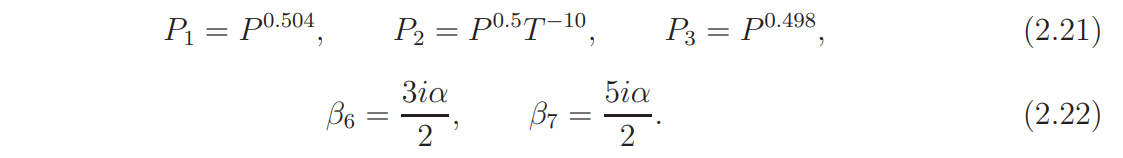
(The definition of β4 and β5 will be given in Section 8.) Write
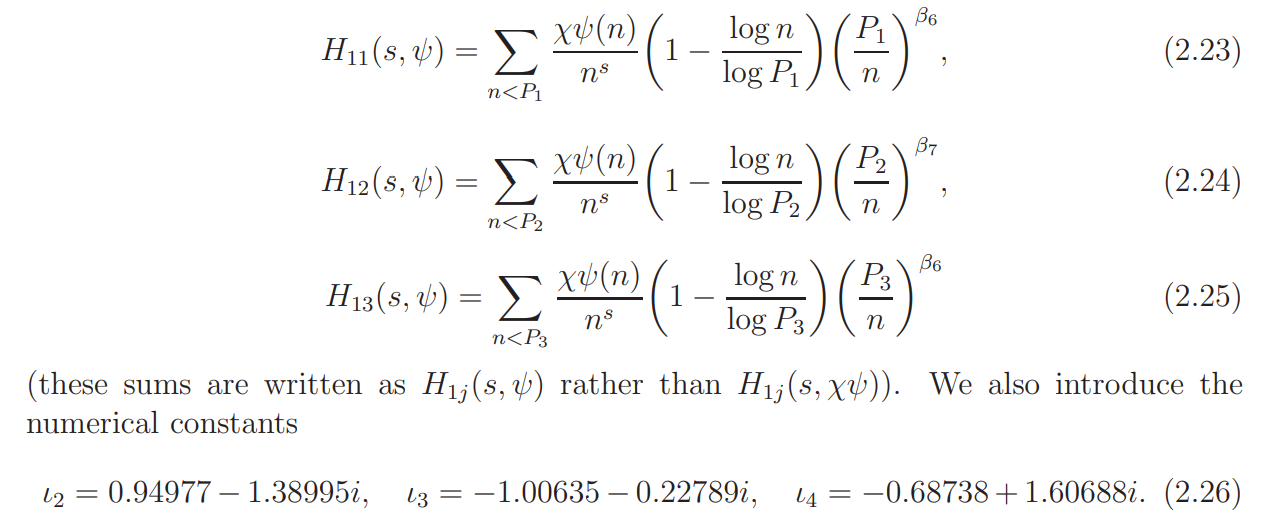
We define
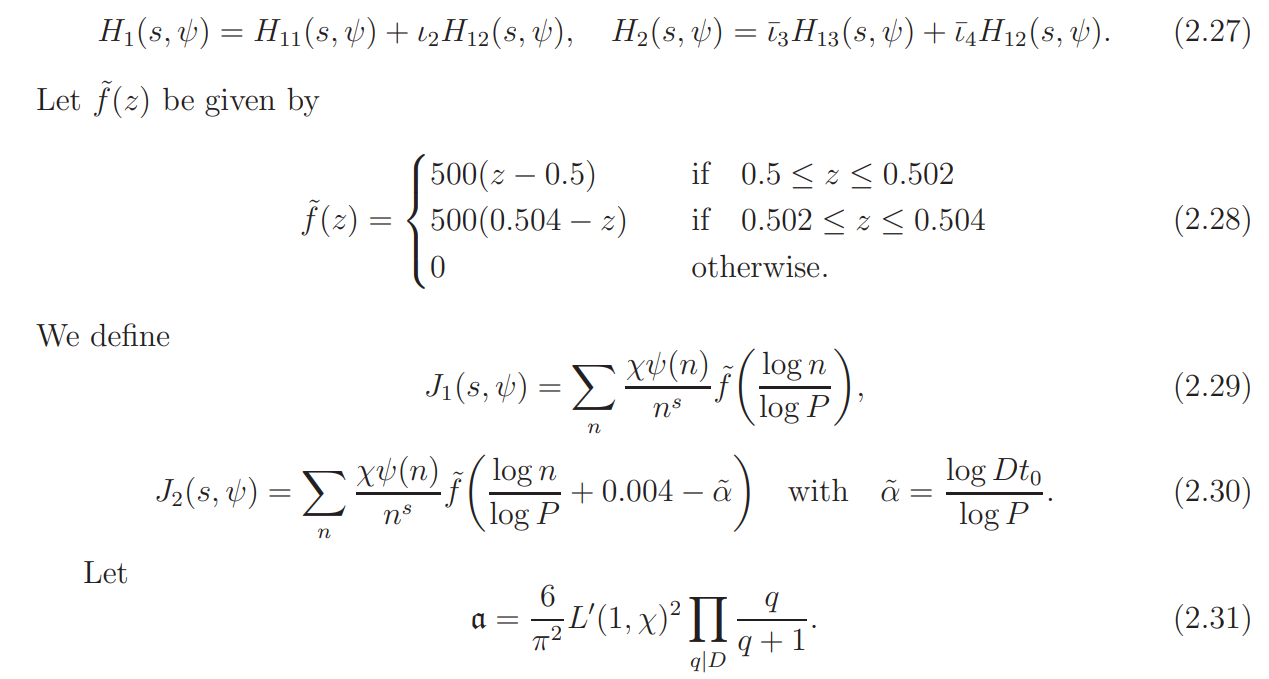
It can be shown that the assumption (A) implies
a ≫ 1.
(see Lemma 5.7).
Proposition 2.4. Assume that (A) holds. Then
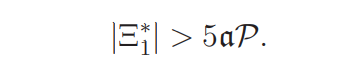
Proposition 2.5. Assume that (A) holds. Then
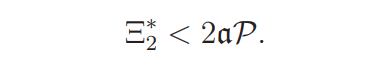
Proposition 2.6. Assume that (A) holds. Then
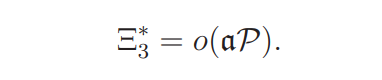
Under Assumption (A), a contradiction is immediately derived from (2.18), Proposition 2.4, 2.5 and 2.6, This proves Theorem 1.
It should be remarked that Proposition 2.5 follows from the inequalities (on assuming (A))
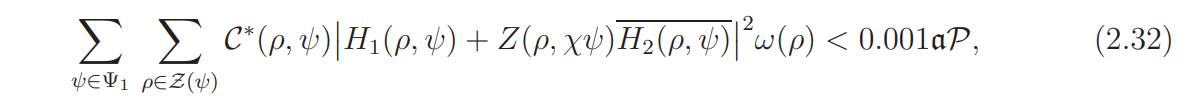
and
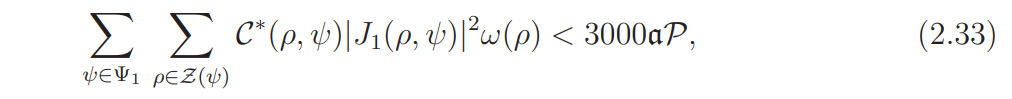
by Cauchy’s inequality (and Lemma 2.3). The proof of (2.32) involves some numerical calculations.
We conclude this section by proving Lemma 2.3.
Proof of Lemma 2.3. By (2.) we see that M(ρ + iv, ψ) 6= 0 if |β2| ≤ v ≤ |β3|. This implies, by the mean-value theorem, that
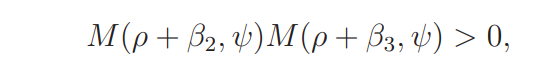
since M(1/2 + it, ψ) is a real-valued continuous function in t. Similarly we have
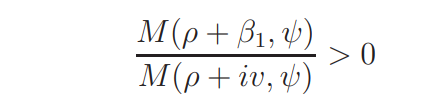
if 0 < v ≤ |β1|. Since
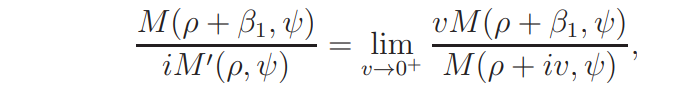
it follows that
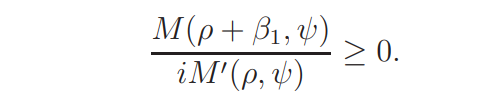
This completes the proof.
Remark. It is implied in the proof of Lemma 2.3 that
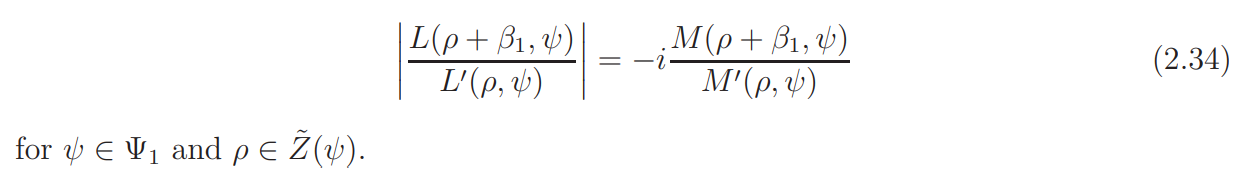
This paper is available on arxiv under CC 4.0 license.

