Why Equivariance Outperforms Invariant Learning in Continual Learning Tasks

Table of Links

Abstract and 1. Introduction

2. Two problems with the current approach to class-incremental continual learning

3. Methods and 3.1. Infinite dSprites

3.2. Disentangled learning

4. Related work

4.1. Continual learning and 4.2. Benchmarking continual learning

5. Experiments

5.1. Regularization methods and 5.2. Replay-based methods

5.3. Do we need equivariance?

5.4. One-shot generalization and 5.5. Open-set classification

5.6. Online vs. offline

Conclusion, Acknowledgments and References

Supplementary Material

5.3. Do we need equivariance?

By training a network to regress the value of each FoV, we learn a representation that is equivariant to affine transformations. However, we could also take advantage of the shape labels to learn an invariant representation that we could then use to perform classification. In this section, we directly compare equivariant and invariant learning to demonstrate further that learning an equivariant representation is the key to achieving effective continual learning within our framework.

Our baseline for invariant representation learning is based on SimCLR [5], a simple and effective contrastive learning algorithm that aims to learn representations invariant to data augmentations. To adapt SimCLR to our problem, we introduce two optimization objectives. The first objective pulls the representation of each training point towards the representation of its exemplar while repelling all other training points. The second objective encourages well-separated exemplar representations by pushing the representations of all exemplars in the current task away from each other. We observed that the first training objective alone is sufficient, but including the second loss term speeds up training. For each task, we train the baseline until convergence. At test time, the class labels are assigned through nearest neighbor

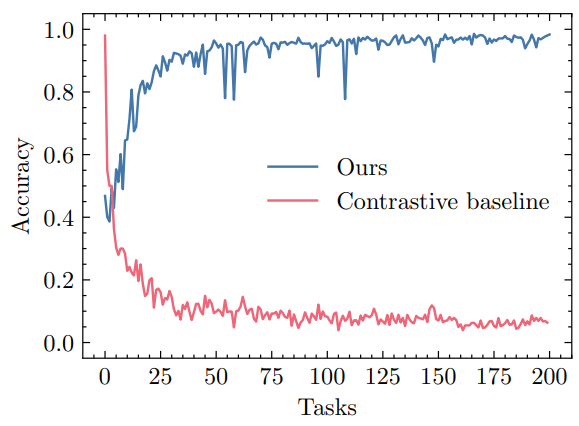
lookup in the representation space. Similar to our method, we store a single exemplar per class.

Figure 6 shows test accuracy for both methods over time. The performance of the contrastive learning baseline decays over time, but not as rapidly as naive fine-tuning. Note that in contrast to our method, invariant learning could benefit from storing more than one exemplars per class. The supplementary material provides an exact formulation of the contrastive objective and implementation details.