Authors:
(1) Sebastian Dziadzio, University of Tübingen ([email protected]);
(2) Çagatay Yıldız, University of Tübingen;
(3) Gido M. van de Ven, KU Leuven;
(4) Tomasz Trzcinski, IDEAS NCBR, Warsaw University of Technology, Tooploox;
(5) Tinne Tuytelaars, KU Leuven;
(6) Matthias Bethge, University of Tübingen.
Table of Links
2. Two problems with the current approach to class-incremental continual learning
3. Methods and 3.1. Infinite dSprites
4.1. Continual learning and 4.2. Benchmarking continual learning
5.1. Regularization methods and 5.2. Replay-based methods
5.4. One-shot generalization and 5.5. Open-set classification
Conclusion, Acknowledgments and References
5. Experiments
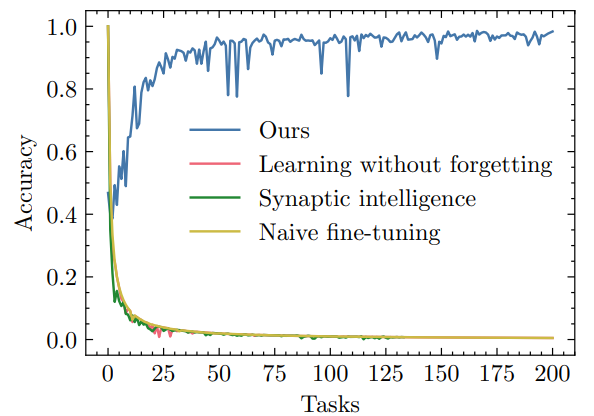
In this section, we evaluate standard continual learning methods and our disentangled learning framework on a benchmark generated using idSprites. The benchmark consists of 200 classification tasks. For each task, we randomly generate 10 shapes and create an image dataset showing the shapes in all combinations of 4 FoVs with 8 possible values per factor. This gives us 40,960 samples per task, which we then randomly split into training, validation, and test sets with a 98:1:1 ratio. The test set is being accumulated at each task until it reaches the maximum limit of 50,000 samples, at which point we employ reservoir sampling to include new classes while keeping the test set bounded and balanced. After training on each task, we report test accuracy on the accumulated test set. To ensure a reliable comparison, we use the same backbone (ResNet-18 [9]) for every method. We also make sure that all models are trained until convergence.
We aim to position our approach among existing continual learning methods, as well as understand its generalization properties. More concretely, the experiments answer the following questions:
• (Section 5.1) How does our approach compare to regularisation-based continual learning baselines?
• (Section 5.2) How does our approach compare to replaybased continual learning baselines? How is the performance of replay affected by memory buffer size and computational budget?
• (Section 5.3) Do we need equivariance or is learning invariant representations enough?
• (Section 5.4) Is our approach able to generalise instantly to previously unseen shapes?
• (Section 5.5) Can our approach perform open-set classification, i.e. distinguish between new and previously seen shapes?
• (Section 5.6) Can we use our approach in the online learning scenario, where each sample from the training stream is observed only once?
This paper is available on arxiv under CC 4.0 license.

